Как начертить эллипс, КОМПАС-3D v21
Однако не всё так гладко…. В рисунке это должно быть хорошо видно и логически осмысленно. Автор комментария: Владимир Дата: Спасибо в ремонте очень пригодилось! Автор: Moroz Дата: Эллипс - геометрическая фигура. Он долго рисовал их на доске и подробно объяснял, как рисовать не надо.

Полуоси эллипса a и b представляют собой расстояния от конца стержня до шарниров на ползунах. Обычно расстояния a и b можно варьировать, и тем самым менять форму и размеры вычерчиваемого эллипса. Содержание переместить в боковую панель скрыть. Учебник Обсуждение.
Читать Править История. Инструменты Инструменты. С помощью циркуля [ править ] Раствором циркуля, равным a , с центром в точке O отметим на одной из прямых точки P 1 и Р 2 , а на второй прямой раствором, равным b — точки Q 1 и Q 2. Полученные точки являются вершинами эллипса , а отрезки P 1 Р 2 и Q 1 Q 2 — его большая и малая оси , соответственно. Полученные точки являются фокусами эллипса.
На отрезке P 1 Р 2 выберем произвольную точку T. Затем с помощью циркуля начертим две окружности: первую — радиуса, равным длине отрезка TP 1 , с центром в точке F 1 и вторую радуса, равным длине отрезка TP 2 , с центром в точке F 2. Точки пересечения этих окружностей принадлежат искомому эллипсу, так как сумма расстояний из обоих фокусов равна длине большой оси 2a. Повторяя необходимое число раз шаги предыдущего пункта, получим искомый эллипс.
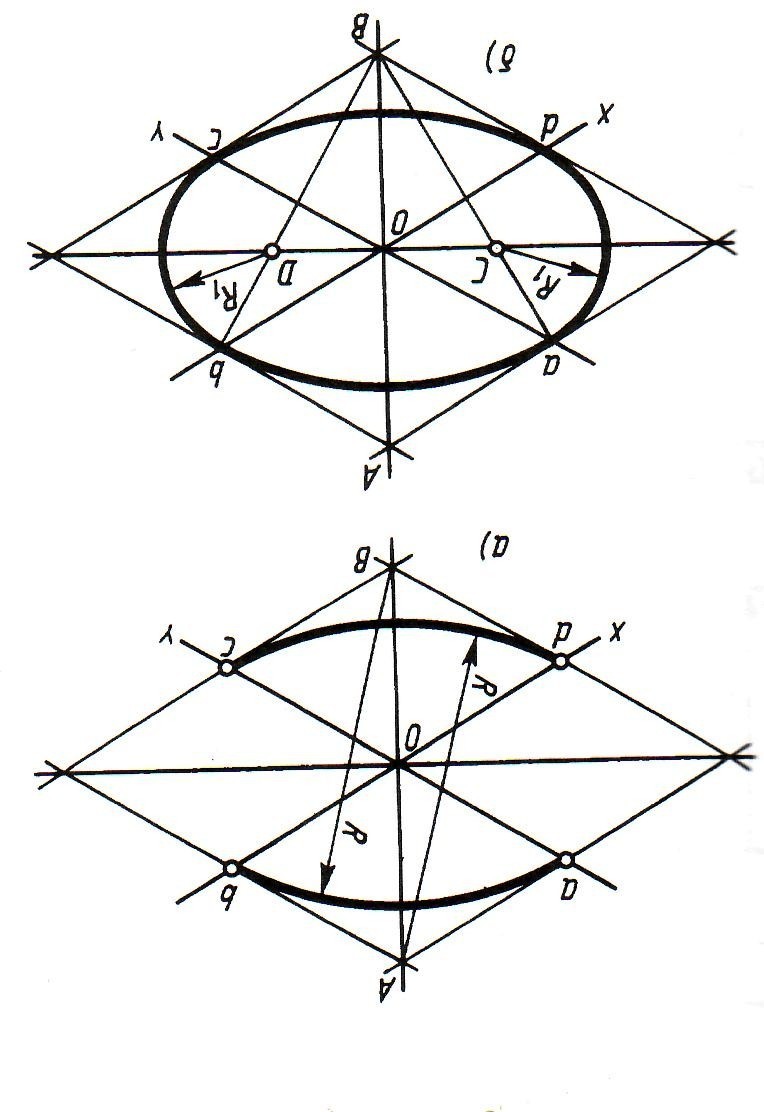
С помощью циркуля и линейки [ править ] Раствором циркуля, равным a , с центром в точке O отметим на одной из прямой точки P 1 и Р 2 , а на второй прямой раствором, равным b — точки Q 1 и Q 2. С помощью линейки проводим через точку O произвольную наклонную линию. Затем раствором циркуля, равным а , с центром в точке O отмечаем на ней точку S , а раствором, равным b — точку R.
Затем из точки S опускаем перпендикуляр на прямую P 1 Р 2. Аналогичным способом опускаем перпендикуляр из точки R на прямую Q 1 Q 2. Поэтому есть разница, с какой именно точки и высоты мы смотрим на объект: рисуем сидя или стоя.
Помните, что линия горизонта всегда находится на уровне ваших глаз. Дело в том, что одна из половинок эллипса ближайшая к нам часть круга визуально крупнее, чем другая половина. Тут вступает в силу закон линейной перспективы: чем ближе к нам объекты, тем они крупнее. По мере удаления от зрителя, они выглядят более мелкими. Вспомните деревья вдоль аллеи: в глубине они кажутся более низкими, чем те, которые находятся непосредственно рядом с наблюдателем.

С половинками эллипса всё то же самое, только это не так сильно заметно. Поэтому при построении эллипса, серединную горизонтальную линию следует расположить чуть выше середины, если линия горизонта над объектом и чуть ниже, если она под объектом таким образом передняя половинка эллипса в рисунке станет выглядеть немного крупнее дальней. А вот правая и левая части эллипса всегда одинаковы.
Постарайтесь избежать любого искажения или неровности в одной из половин - они зеркальное отражение друг друга. Чтобы визуально было проще представить раскрытие плоскости и сокращение её в глубину, можно наметить для себя условные боковые направляющие.
Это даст ощущение пространства и чувство ухода плоскости в глубину от зрителя. Ещё один вариант, помогающий соблюсти симметрию правой и левой частей эллипса наиболее точно и позволяющий доказать правильность расположения серединной горизонтальной линии - проведение диагоналей при построении. Для этого зафиксируем левую и правую вершины рассматриваемого эллипса, то есть, значение большой полуоси будет оставаться постоянным.
Тогда формула эксцентриситета примет вид:. Начнём приближать значение эксцентриситета к единице. Это возможно только в том случае, если. Что это значит? Это значит, что фокусы эллипса будут «разъезжаться» по оси абсцисс к боковым вершинам. И, поскольку «зелёные отрезки не резиновые», то эллипс неизбежно начнёт сплющиваться, превращаясь всё в более и более тонкую сосиску, нанизанную на ось. Таким образом, чем ближе значение эксцентриситета эллипса к единице, тем эллипс более продолговат.
Теперь смоделируем противоположный процесс: фокусы эллипса пошли навстречу друг другу, приближаясь к центру. Это означает, что значение «цэ» становится всё меньше и, соответственно, эксцентриситет стремится к нулю:. При этом «зелёным отрезкам» будет, наоборот — «становиться тесно» и они начнут «выталкивать» линию эллипса вверх и вниз.
Таким образом, чем ближе значение эксцентриситета к нулю, тем эллипс больше похож на … смотрим предельный случай , когда фокусы успешно воссоединились в начале координат:. Окружность — это частный случай эллипса Действительно, в случае равенства полуосей каноническое уравнение эллипса принимает вид , который рефлекторно преобразуется к — хорошо известному из школы уравнению окружности с центром в начале координат радиуса «а». На практике чаще используют запись с «говорящей» буквой «эр»:.
Радиусом называют длину отрезка , при этом каждая точка окружности удалена от центра на расстояние радиуса. Заметьте, что определение эллипса остаётся полностью корректным: фокусы совпали , и сумма длин совпавших отрезков для каждой точки окружности — есть величина постоянная. Так как расстояние между фокусами , то эксцентриситет любой окружности равен нулю.
Строится окружность легко и быстро, достаточно вооружиться циркулем. Тем не менее, иногда бывает нужно выяснить координаты некоторых её точек, в этом случае идём знакомым путём — приводим уравнение к бодрому матановскому виду: — функция верхней полуокружности; — функция нижней полуокружности. После чего находим нужные значения, дифференцируем , интегрируем и делаем другие хорошие вещи. Статья, конечно, носит справочный характер, но как на свете без любви прожить?
Творческое задание для самостоятельного решения. Составить каноническое уравнение эллипса, если известен один из его фокусов и малая полуось центр находится в начале координат. Найти вершины, дополнительные точки и изобразить линию на чертеже. Вычислить эксцентриситет. Вернёмся к каноническому уравнению эллипса , а именно, к условию , загадка которого терзает пытливые умы ещё со времён первого упоминания о данной кривой.
Вот мы рассмотрели эллипс , но разве на практике не может встретиться уравнение? Ведь здесь , однако, это вроде бы как тоже эллипс! Подобное уравнение нечасто, но действительно попадается. И оно действительно определяет эллипс. Развеем мистику: В результате построения получен наш родной эллипс, повёрнутый на 90 градусов.
То есть, — это неканоническая запись эллипса. Как быть, если такое чудо-яйцо всё-таки встретилось на жизненном пути? В том случае если вам предложено построить эллипс, то, наверное, лучше построить его в нестандартном виде. С вершинами и дополнительными точками, думаю, трудностей не возникнет. Но если вам предложено найти фокусы, эксцентриситет и т. Примечание : в теории принято поворачивать не саму фигуру, а оси!
И если от вас требуется именно ПРИВЕСТИ уравнение к каноническому виду , то решение, строго говоря, следует оформить иначе: «Перейдём к новой прямоугольной системе координат , повернув координатные оси на 90 градусов против часовой стрелки, и запишем уравнение эллипса в каноническом виде: ».
Впрочем, эрудиты могут встать на скользкую дорожку путаницы, модифицировав все расчёты с учётом поворота. Но всё равно не советую. Потому что ребячество. Уравнение задаёт эллипс с большой полуосью «а», малой полуосью «бэ» и центром симметрии в точке. Изобразим на чертеже эллипс. Согласно формуле: , то есть наш подопытный эллипс «переехал» в точку : Значения остались прежними, а вот фокусы, разумеется, мигрировали, и формулы их координат нужно модифицировать поправками на соответствующие сдвиги:.
Здесь всё обходится значительно проще, чем при повороте, и если по условию не нужно приводить уравнение к каноническому виду, то лично я предпочту оставить его в виде. Что делать, если нужно приводить? Но академический подход предполагает параллельный перенос не самой фигуры, а системы координат! Уравнение задаёт окружность радиуса с центром в точке.
Освежая ностальгические воспоминания, изобразим на чертеже окружность, заданную уравнением : В исследовательских целях приведём наше уравнение к общему виду, выполнив возведение в квадрат и приведение подобных слагаемых: — как правило, в таком обличье оно и встречается в природе. Таким образом, в практических задачах часто предварительно нужно выполнить обратное действие — выделить полные квадраты.
Данный приём подробно разобран на уроках о геометрических преобразованиях графиков и интегрировании дробей. Хотя следующий простой пример не должен вызвать у вас затруднений даже без отработки данного метода:.
Построить график линии, заданной уравнением.
На практике эллипс как и другие линии может быть одновременно повёрнут на любой угол относительно своего канонического положения и перенесен в любую точку, отличную от начала координат. В таком случае решается типовая задача приведения линии 2-го порядка к каноническому виду , к которой я потихоньку начал вас готовить уже сегодня.
Ну а пока самое время перейти ко второй части лекции, где жертвами станут гипербола и парабола. Пример 2: Решение : поскольку фокусы канонически расположенного эллипса имеют координаты , то расстояние от каждого из фокусов до начала координат равно:.
По условию известно значение , из соотношения находим: Запишем каноническое уравнение эллипса: Вершины эллипса расположены в точках. Найдём дополнительные точки: Выполним чертёж: Вычислим эксцентриситет:. Пример 3: Решение : выделим полный квадрат: — окружность радиуса с центром в точке. Выполним чертёж:.
Как можно отблагодарить автора? Копирование материалов сайта запрещено. Повторяем школьный курс Аналитическая геометрия: Векторы для чайников Скалярное произведение векторов Линейная не зависимость векторов. Уравнение плоскости Прямая в пространстве Задачи с прямой в пространстве Основные задачи на прямую и плоскость Треугольная пирамида Элементы высшей алгебры: Множества и действия над ними Основы математической логики Формулы и законы логики Уравнения высшей математики Как найти рациональные корни многочлена?
Ортогональное преобразование квадратичной формы Пределы: Пределы. Теория Производные функций: Как найти производную? Приближенные вычисления с помощью дифференциала Метод касательных Функции и графики: Графики и свойства элементарных функций Как построить график функции с помощью преобразований? Непрерывность, точки разрыва Область определения функции Асимптоты графика функции Интервалы знакопостоянства Возрастание, убывание и экстремумы функции Выпуклость, вогнутость и точки перегиба графика Полное исследование функции и построение графика Наибольшее и наименьшее значения функции на отрезке Экстремальные задачи ФНП: Область определения функции двух переменных.
Частные производные неявно заданной функции Производная по направлению и градиент функции Касательная плоскость и нормаль к поверхности в точке Экстремумы функций двух и трёх переменных Условные экстремумы Наибольшее и наименьшее значения функции в области Метод наименьших квадратов Интегралы: Неопределенный интеграл.
Дифференциальные уравнения: Дифференциальные уравнения первого порядка Однородные ДУ 1-го порядка ДУ, сводящиеся к однородным Линейные неоднородные дифференциальные уравнения первого порядка Дифференциальные уравнения в полных дифференциалах Уравнение Бернулли Дифференциальные уравнения с понижением порядка Однородные ДУ 2-го порядка Неоднородные ДУ 2-го порядка Линейные дифференциальные уравнения высших порядков Метод вариации произвольных постоянных Как решить систему дифференциальных уравнений Задачи с диффурами Методы Эйлера и Рунге-Кутты Числовые ряды: Ряды для чайников Как найти сумму ряда?
Признак Лейбница Ряды повышенной сложности Функциональные ряды: Степенные ряды Разложение функций в степенные ряды Сумма степенного ряда Равномерная сходимость Другие функциональные ряды Приближенные вычисления с помощью рядов Вычисление интеграла разложением функции в ряд Как найти частное решение ДУ приближённо с помощью ряда? Примеры решений Кратные интегралы: Двойные интегралы Как вычислить двойной интеграл?
Работа силы Поверхностные интегралы Элементы векторного анализа: Основы теории поля Поток векторного поля Дивергенция векторного поля Формула Гаусса-Остроградского Циркуляция векторного поля и формула Стокса Комплексный анализ: ТФКП для начинающих Как построить область на комплексной плоскости?
Теория вероятностей: Основы теории вероятностей Задачи по комбинаторике Задачи на классическое определение вероятности Геометрическая вероятность Задачи на теоремы сложения и умножения вероятностей Зависимые события Формула полной вероятности и формулы Байеса Независимые испытания и формула Бернулли Локальная и интегральная теоремы Лапласа Статистическая вероятность Случайные величины.
Равномерное распределение Показательное распределение Нормальное распределение Система случайных величин Зависимые и независимые случайные величины Двумерная непрерывная случайная величина Зависимость и коэффициент ковариации непрерывных СВ Математическая статистика: Математическая статистика Дискретный вариационный ряд Интервальный ряд Мода, медиана, средняя Показатели вариации Формула дисперсии, среднее квадратическое отклонение, коэффициент вариации Асимметрия и эксцесс эмпирического распределения Статистические оценки и доверительные интервалы Оценка вероятности биномиального распределения Оценки по повторной и бесповторной выборке Статистические гипотезы Проверка гипотез.
Так вот, какую бы точку эллипса мы ни взяли, сумма длин отрезков всегда будет одной и той же: Убедимся, что в нашем примере значение суммы действительно равно восьми.
Вычисления проще пареной репы:! Едем дальше: Эксцентриситет эллипса и его геометрический смысл Эксцентриситетом эллипса называют отношение , которое может принимать значения в пределах. В нашем случае: Выясним, как форма эллипса зависит от его эксцентриситета.
Найдём дополнительные точки: Выполним чертёж: Вычислим эксцентриситет: Пример 3: Решение : выделим полный квадрат: — окружность радиуса с центром в точке. Виды и примеры решений Коэффициент ранговой корреляции Спирмена Коэф-т корреляции Фехнера Уравнение множественной линейной регрессии Не нашлось нужной задачи?